Незважаючи на те, наскільки розумними ми є як вид, Мати Природа майже завжди здається розумнішою за нас. Це стосується і мозкової хірургії, і робототехніки, і навіть спроби уникнути теплової смерті планети. І, як виявилося, це також стосується й математики високого рівня.
«Центральною проблемою геометрії є заповнення простору простими структурами», — починається нова стаття, опублікована цього тижня дослідниками Оксфордського університету, в якій йдеться про відкриття нової класифікації форм під назвою «м’які клітини».
«Класичні рішення, такі як трикутники, квадрати та шестикутники на площині та куби та інші багатогранники у тривимірному просторі, мають гострі кути та плоскі грані», — пишуть автори. «Однак багато природних укладок характеризуються формами з кривими краями, неплоскими гранями і з мінімумом, якщо взагалі, гострих кутів».
Основна проблема полягає в наступному: як краще заповнити простір формами або об’єктами? Коли це питання ставлять перед людиною, ми інстинктивно обираємо форми з гострими кутами — квадрати, трикутники, шестикутники, подібні речі. Це логічно, адже спробуйте заповнити простір колами — і ви неминуче отримаєте порожні місця, незалежно від того, наскільки дрібно або складно їх укладати.
Але коли ми дивимося на те, як природний світ відповів на це питання, то практично не зустрічаємо подібних рішень. Як зазначає професор математичного моделювання Оксфордського університету Ален Гор’єлі, один із авторів нової статті: «Природа не лише ненавидить вакуум, вона, здається, ненавидить і гострі кути».
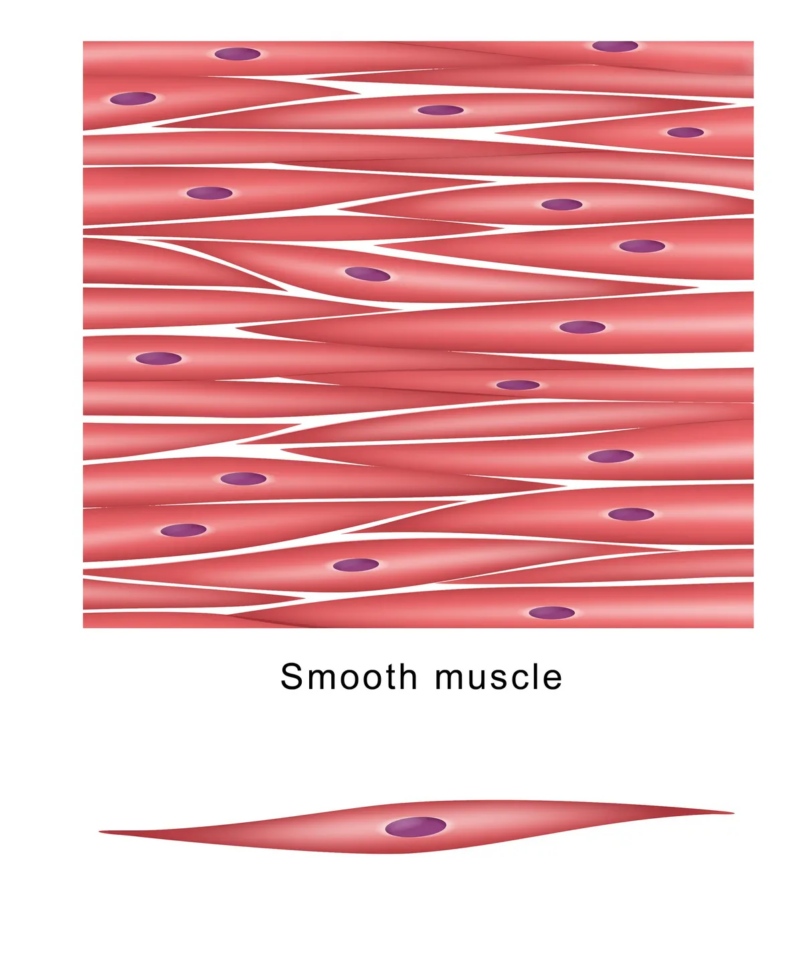
Візьмемо, наприклад, цибулю. Розріжте її навпіл, і ви побачите ідеально упаковану колекцію взаємопов’язаних форм, але, звісно, без прямих кутів або ліній. Так само і з м’язовою тканиною: якщо подивитися на поперечний зріз клітин, які складають гладкі м’язові волокна, ви побачите мозаїку сплющених кіл, довгих і тонких, з загостреними кінцями.
Звісно, це не означає, що ніхто раніше не помічав ці форми або того, що це зручний спосіб заповнення простору без залишкових порожнин. Але як саме вони працюють з математичної точки зору? Це залишалося загадкою.
«Хоча комбінаторні властивості укладок були досліджені детально, менше уваги приділялося плавності клітин», — пояснюється в статті. «Оскільки шматкоподібні гладкі форми, такі як квадрати та куби, дійсно заповнюють простір, а плавні форми не можуть, природно виникає питання, наскільки гладкими можуть бути форми, що заповнюють простір».
Це дещо технічно складно, але суть така: якщо форма недостатньо «гостра», то вона просто не зможе заповнити простір. Відповідно, завданням команди було визначити, наскільки гострою мінімально повинна бути форма, щоб успішно заповнювати простір.
Рішенням стали так звані «м’які клітини». Це форми, які «мінімізують кількість гострих кутів», — пояснюють вони в статті, — «заповнюючи простір м’якими укладками […] Цікаво, що ці ідеальні м’які форми, народжені з геометрії, у великій кількості зустрічаються в природі — від клітин до мушель».
Ці форми особливо цікаві, коли ми переходимо від двох вимірів до трьох. «М’які клітини допомагають пояснити, чому, коли ви дивитеся на поперечний зріз камерної мушлі, то бачите кути, але тривимірна геометрія камер не має їх», — пояснює професор геометричного моделювання Будапештського університету технологій та економіки Габор Домокос, один із співавторів статті.
Насправді, як і з багатьма іншими відкриттями, ці форми можна знайти всюди, якщо ви знаєте, де шукати. Вони є «геометричними будівельними блоками біологічної тканини», пояснює команда, формуючи такі поширені природні форми, як клітини, річкові острови та мушлі.
«Створення та підтримання гострих кутів у фізичних клітинах є складним і дорогим», — пишуть дослідники, — «оскільки поверхневий натяг і еластичність природним чином мають тенденцію згладжувати кути. Тому не дивно, що багато м’яких укладок зустрічаються в природі».
«Відсутність гострих кутів і їхня м’яка, дуже вигнута геометрія робить м’які клітини ідеальними моделями для біологічних структур, які розвивалися за умов повного або часткового обмеження для заповнення простору», — роблять висновок дослідники.
Стаття була опублікована в журналі PNAS Nexus.
